Draw a neat labelled sketch of fuel injection pump. Give its function.
Fuel injection pump : Fuel injection pump is used widely for the supply of fuel under high pressure in diesel engines


Fuel injection pump : Fuel injection pump is used widely for the supply of fuel under high pressure in diesel engines

Classification of gas turbine on the basis of
a. Cycle of operation 1. Open cycle 2. Closed cycle
b. Thermodynamic cycle 1. Brayton or Joules cycle 2. Atkinson cycle 3. Erricsson cycle
c. Application 1. For supercharging of IC engine 2. For locomotive propulsion 3. For ship propulsion 4. Industrial application 5. Air craft engines 6. Electric power generation
d. Combustion process 1. Continuous combustion 2. Explosion combustion
Classification of Air compressors:
1. According to principle: a) Reciprocating air compressors b) Rotary air compressors 2. According to the capacity a. Low capacity air compressors b. Medium capacity air compressors c. High capacity air compressors 3. According to pressure limits a. Low pressure air compressors b. Medium pressure air compressors c. High pressure air compressors 4. According to method of connection a. Direct drive air compressors b. Belt drive air compressors c. Chain drive air compressors
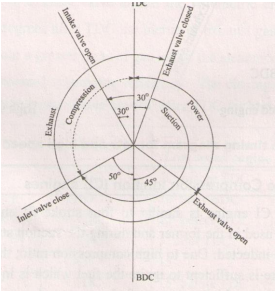
Valve timing diagram of four stroke diesel engine
Diesel Cycle on P-V and T-S diagram :
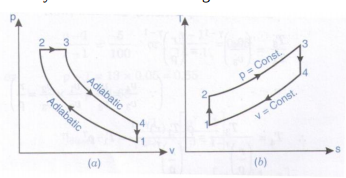
Processes : 1-2 : Isentropic compression 2-3 : Heat addition at constant pressure 3-3 Isentropic expansion 4-1 Heat rejection at constant volume
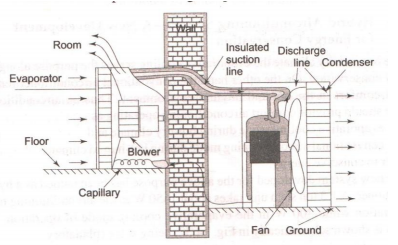
Split Air-conditioner labeled Diagram 02 for figure 02 for labeling
Ram jet – (Fig – 2 marks ; explanation –2 marks) - Ram jet is also called as ‘Athodyd or flying stove pipe’. - It is a steady combustion or continuous flow engine & has the simplest construction of any propulsion engine. - Consist of inlet diffuser, combustion chamber & exit nozzle. - Air entering into ram jet with supersonic speed is slowed down to sonic speed in supersonic diffuser, increasing air pressure. - The air pressure is further increased in the subsonic diffuser. - The fuel injected into the combustion chamber is burned with the help of flame stabilizers.
i) DPT – Dew point temperature tDP - It is the temperature at which air water vapour mixture starts to condense. D.P.T. of mixture is defined as the temperature at which water vapours starts to condense.
Ii) WBT - Wet bulb temperature - tWB - It is the temperature recorded by thermometer when its bulb is covered with wet cloth known as wick and is exposed to air.
Necessity of purification of air in compressor :