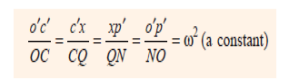Explain the Klein's construction to determine velocity and acceleration of single slider crank mechanism.

We have already discussed that the velocity diagram for given configuration is a triangle OCP as shown in Fig. If this triangle is rotated through 90°, it will be a triangle oc1 p1, in which oc1 represents VCO (i.e. velocity of C with respect to O or velocity of crank pin C) and is parallel to OC, op1 represents VPO (i.e. velocity of P with respect to O or velocity of cross-head or piston P) and is perpendicular to OP, and c1p1 represents VPC (i.e. velocity of P with respect to C) and is parallel to CP. A little consideration will show that the triangles oc1p1 and OCM are similar. Therefore,
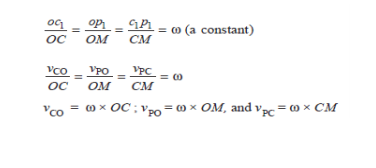
Thus, we see that by drawing the Klein’s velocity diagram, the velocities of various points may be obtained without drawing a separate velocity diagram. Klien’s acceleration diagram: The Klien’s acceleration diagram is drawn as discussed below: 1. First of all, draw a circle with C as centre and CM as radius. 2. Draw another circle with PC as diameter. Let this circle intersect the previous circle at K and L. 3. Join KL and produce it to intersect PO at N. Let KL intersect PC at Q. This forms the quadrilateral CQNO, which is known as Klien’s acceleration diagram. We have already discussed that the acceleration diagram for the given configuration is as shown in Fig. We know that (i) o'c' represents CO ar (i.e. radial component of the acceleration of crank pin C with respect to O ) and is parallel to CO; (ii) c'x represents PC ar (i.e. radial component of the acceleration of crosshead or piston P with respect to crank pin C) and is parallel to CP or CQ; (iii) xp' represents PC at (i.e. tangential component of the acceleration of P with respect to C ) and is parallel to QN (because QN is perpendicular to CQ); and (iv) o'p' represents aPO (i.e. acceleration of P with respect to O or the acceleration of piston P) and is parallel to PO or NO. A little consideration will show that the quadrilateral o'c'x p' is similar to quadrilateral CQNO . Therefore,