A 4-bar mechanism has following dimensions:
l(DA)= 300 mm l(CB) = l(AB) = 360 mm
l(DC) = 600 mm. The link ‘DC’ is fixed. The angle ADC
is 60°
The driving link ‘DA’ rotates at a speed of 100 rpm
clockwise and constant driving torque is 50 N.M. Calculate
the Velocity of point ‘B’ and angular velocity of driven link
‘CB’.
A 4-bar mechanism has following dimensions:
l(DA) = 300 mm, l(CB) = l(AB) = 360mm, l(DC) = 600 mm. the link ‘DC’ is fixed. The
angle ADC is 60o. The driving link ‘DA’ rotates at a speed of 100 rpm clockwise and
constant driving torque is 50 N-m. Calculate the velocity of point ‘B’ and angular
velocity of driven link ‘CB’.
Given Data:
N AD = 100 rpm
DA = 300 mm = 0.3 m
T A = 50 N-m
ω AD = 2 π x 100 /60 = 10.47 rad/sec.
Velocity of A w.r.t. D (V AD);
Velocity of Point B:
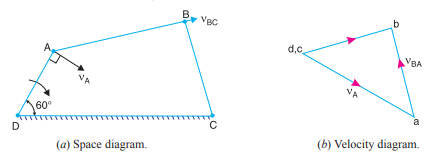
[1] Since the link DC is fixed, therefore points d and c are taken as one point in the
velocity diagram. Draw vector da perpendicular to DA, to some suitable scale, to
represent the velocity of A with respect to D or simply velocity of A (i.e. V AD or V A ) such
that,
Vector da =V AD = V A = 3.14 m/s
[2] Now from point a, draw vector ab perpendicular to AB represents the velocity of B
with respect to A (i.e. V BA ), and from point c draw vector cb perpendicular to CB to
represent the velocity of B with respect to C or simply velocity of B (i.e. V BC or V B ). The
Vectors ab and cb intersect at b.
[3] By measurement, we find that velocity of point B,
V B = V BC = vector cb = 2.25 m/s
[4] Angular Velocity of driven link CB
Since CB = 360 mm =0.36 m, therefore angular velocity of the driven link CB,
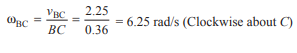
marks:
- Log in to post comments
