A bracket as shown in Figure No. 1 is fixed to a vertical steel column by means of five standard bolts.

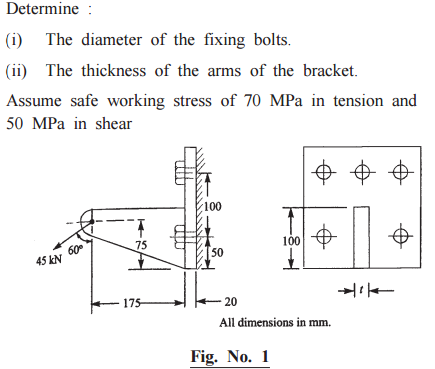
Horizontal component of 45 KN, WH= 45Sin 600 =45x 0.866=38971N and vertical component of 45 KN, Wv,= 45xcos600 =45x0.5=22500N Direct tensile load in each bolt,Wt1= WH /5=38971/5=7794.20N Turning moment due to WH about G TH = WHx 25=38971x25=974275N (anticlockwise) direct shear load on each bolt =Ws=Wv/5 =22500/5=4500N Turning moment due to Wv about edge of the bracket, Tv= Wvx175=22500x175=3937500N-mm( clockwise( clockwise) Net turning moment =3937500-974275=2963225N---------(I) total moment of the load on the bolts @ th tilting edge = 2w x(L1) 2 + 2w x(L2) 2 =2xwx(50)2 + 2xwx(150)2 = 50000 w N-mm-----(II) from equations (I) and(II) 2963225N=50000 w N- w= 592.645 N max. tensile load on each of the upper bolt, Wt2= wL2 =592.645x150=88896.75 N tensile load on each of the upper bolt, Wt = Wt1+ Wt2 =7794.20+ 88896.75=96690.95N equivalent tensile load =Wte=1/2(Wt+ √‾(Wt)2 + 4(Ws)2 =1/2 ( 96690.95+97108.91)=96899.93 N Tensile load on each bolt = ∏/4(dc)2 x 6t =0.7854x(dc)2 x 70 dc = 41.98 mm from coarse series the standard core dia. Is 49.0177 mm and corresponding size of the bolt is M56 thickness of the arm of the bracket cross sectional area of the arm A = bXt =100x t

section modulus of the arm, Z = 1/6 t (b)2 = 1/6 xtx(100)2 =1666.67 xt direct tensile stress 6t1 = WH/A = 38971/100t =389.71/t bending stress 6t2 = MH/Z = 208/t bending stress 6t3 = Mv /Z = 2632.49/t net tensile stress, 6t1 +6t2 + 6t3 = 3230.20/t max. tensile stress , 6t max. 6t/2+ ½ √‾(6t)2 + 4(Ʈ)2 =70 t = 46.36 mm