Four masses attached to a shaft and their respective radii of rotation are given as :
m 1 = 180 kg m 2 = 300 kg m 3 = 230 kg m 4 = 260 kg
r 1 = 0.2 m r 2 = 0.15 m r 3 = 0.25 m r 4 = 0.3 m
The angles between successive masses are 45, 75 and 135. Find the
position and magnitude of the balance mass required, it its radius of rotation is
0.2 m. The masses revolve in same plane.
Given : m1 = 180 kg, m2 = 300 kg, m3 = 230 kg, m4 = 260 kg r1 = 0.2 m, r2 = 0.15 m, r3 = 0.25 m, r4 = 0.3 m ϴ1 = 45, ϴ2 = 75, ϴ = 135 The centrifugal forces are given by - m1r1 = 36, m2r2 = 45, m3r3 = 57.5, m4r4 = 78
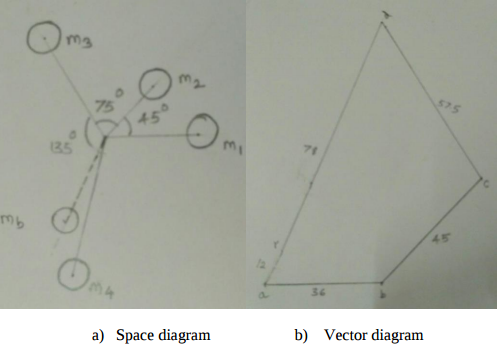
From vector diagram the resultant force is at 60 to the mass m1 and is represented by ar ar = 12 kg m Therefore mb * rb = 12 kgm Balancing mass mb = 12/0.2 = 60 kg at an angle of 2400 with the direction of m1 mass
