Theory question and answers on Fluctuating Stresses
Q.1. What are the various factor that reduce fatigue strength of the material? What factors should be considered while designing against fatigue failure? How the endurance limit for a given component is obtained from the endurance limit from standard test?
Ans : Factors affecting fatigue strength of a material are as follows,
1) Surface finish factor ( Ka) : The surface of the test specimen is polished to mirror finish in axial direction to smooth out any circumferential scratches, but actual component in a machine amy not have such finish. When the surface finish is poor, there are scratches on the surface which act as stress raisers, and reduce the fatigue strength. This is taken into account through surface finish factor ka.
2) Size Factor (Kb) : The diameter of the test specimen in Fatigue test is generally 7.5 mm, where as the size of actual component may be very larger than this size. As the size increases there is greater probability that the surface defects may exist in the component. It mean the chances of fatigue failure at any of these defects is more. Hence the endurance limit of component reduces with the size of the component.
3) Load Factor or Reliability factor (Kc) : The laboratory values of endurance limit are usually mean values. There is considerable dispersion of the data when a number of tests are conducted even using the same material and conditions.The reliability factor takes into accoun this probability that the component will survive given set of conditions.
4) Modifying factor for stress concentration (Kd) : stress concentration has very negative effect on endurance limit of a material to apply this effect modifying factor for stress concentration is taken into account, which factor is denoted by Kd .
so accordingly considering all these factors the endurance limit for a given component is computed by formula,
Where se = Endurance limit for the given component and se' = Endurance limit obtained from standard speciment test for given material.
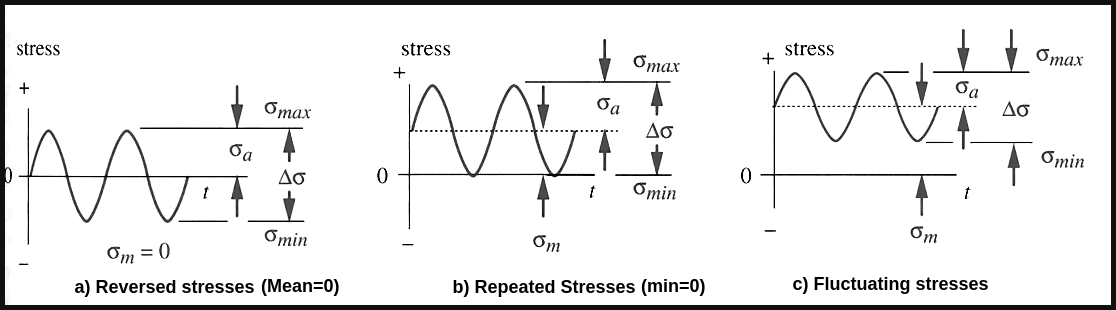
Q.2. Explain fluctuating stress,repeated stresses and reversed stresses. Draw diagram for each type of stress.
Ans : Fluctuating stresses : The components may be subjected to the forces, which are not static in magnitude, but vary in magnitude with respect to time. The stressinduced due to such forces are called fluctuating stresses.the fluctuating stresses have maximum stress value, or minimum stress value and the mean of both of them. the stress fluctuates between two limit, maximum and minimum stress. most of the components failed due to fatigue failure resulting from fluctuating stresses.
Repeated stresses : The repeated stresses are a particular case of fluctuating stresses where the minimum stress is zero, in other words the variation of repeated stresses is from zero to some maximum value. The minimum stress is zero and therefore the amplitude and maximum stress are numerically equal.
Reeversed stresses : The reversed stresses are a particular case of fluctuating stresses where the average stress is zero, in other words the variation of repeated stresses is on both sides of zero of equal magnitude. The average stress is zero and therefore the amplitude is twice the maximum stress .
Q.3. What is Notch sensitivity? Why it is required? what are its extreme values for fully sensitive and no sensitive material to notch effects?
Ans : Notch Sensitivity : it is practically observed that the actual reduction in in durance limit of a material due to stress concentration is less than the amount indicated by theoretical stress concentration factor, which is denoted by Kt . so if we use the factor Kt , for deciding the actual endurance limit of a component, it will give a very smaller value of endurance limit. In order to avoid this a separate stress concentration factor is defined as Kf ,which is called fatigue stress concentration factor,
Here comes a need to define a property of material to respond to the notches, it is called the Notch sensitivity.
"Notch sensitivity is defined as the probability of a material to fail to the damaging effect of stress raising notches under fatigue load."
It is used to relate between the theorotical stress concentration factor Kt and Fatigue stress concentration factor Kf.
For a fully sensitive material Kf will be equal to Kt, so q=1 {means that there is 100% probability of material failing due to damaging effect of stress raising notches under fatigue load)
For a non sensitive material Kf=1 , q=0. {means that there is 0% probability of material failing due to damaging effect of stress raising notches under fatigue load)
Q.4. What is Miner's Equation? Where do you use Miner's Equation?
Ans : Miner's equation is applicable to the components which are subjected to different stress levers (completely reversed stresses) for various parts of life cycles. It is called the cumulative fatigue damage.
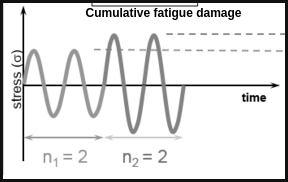
Suppose a component is subjected to completely reversed stress for n1 cycles,
for n2 cycles,
for n3 cycles, and
for n4 cycles and let N1,N2,N3 and N4 be the number of stress cycles befor fatigue failure when the respective stresses are acting alone. Then according to Miner,
Using the above equation the life to the component subjected to different stress levels can be determined.
Limitations : Miner's equation assumes that the damage to the component is directly proportional to the number of cycles at a given stress value. It also assumes that the sequence in which stresses are applied does not matter. Both of these assumptions are not completely verified in the tests. In some circumstances, cycles of low stress followed by high stress cause more damage than would be predicted by the Miner's equation.
Problems on Fluctuating Stresses
1)A rod of a linkage mechanism made of steel 40Crl(Sut =550MPa) is subjected to a completely reversed axial load OF 1000 kN. The rod is machined on a lathe and the reliability is 90%. There is no stress concentration. Determine the diameter of the rod using a factor of safety of 2 for an infinite conditions. Assume K a = 0.78 , K b = 0.85, for 90% reliability = 0.868.
2) A transmission shaft of cold drawn steel is subjected to a fluctuating torque which varies from-100 N-m to 400 N-m. The factor of safety is 2 and the expected reliability is 90%. Neglecting the effect of stress concentration,
determine the diameter of the shaft. Assume the distortion energy theory of failure. S ut = 500MPa, S yt = 300MPa.
3) A rod linkage mechanism is made up of steel 40Cr1 (Sut= 500 N/mm2) is subjected to a completely reversed axial load of 100 kN. The rod is machined on a lathe and the expected reliability is 95%. There is no stress concentration . Determine the diameter of rod using a factor of safety 2 considering infinite life condition.
4) A rotating bar is made up of steel 45C8 having ultimate tensile stress 630 N/mm2 is subjected to completely reversed bending stresses. Calculate the fatigue strength of the bar for a life of 90000 cycles if the corrected endurance limit is 315 N/mm2.
5) A steel bar having 50 mm diameter is subjected to a reversed beding stress of 250 N/mm2. The bar is made of steel 40C8 ( Sut =600 N/mm2). Find the Life of component in cycles for the reliability of 90%.
6) A cold drawn steel bar is subjected to varying bending moment from 565 N-m to 1200 N-m as the axial load also varies from 5000 N to 13500 N. Determine the diameeter of the bar with FOS 2, neglecting the stress concentration effect. Design is to be based on Max shear stress theory
Take Ultimate tensile stress =550 Mpa
Yield strength =470 MPa, Surface finish factor =0.82, size factor =0.8, reliability factor = 0.897
7) A apherical pressure vessel has 500 mm ID. The plates are madeup of cold drawn steel 30c8 hating ultimate stress 440 MPa and yield stress 242 MPa. The vessel is subjected to internal pressure varying from 0 to 6 N/mm2. Taking FOS 3.5, reliability 50%,size factor 0.85, surface finish factor 0.82 respectively. Calulate the thickness of the plate to withstand infinite number of stress cycles.
8) A forged steel bar is 50 mm diameter and is subjected to completely reversed bending stress of 250 N/mm2.The bar is made up of material having ultimate tensile strength 600 Mpa. Taking reliability factor 0.897,size factor 0.85,Surface finish factor 0.43. Determine the life of bar in terms of cycles.
9) A cantilever beam is made up of cold drawn steel having ultimate tensile strength 600 MPa and Yield point stress 380 MPa. It has two diameters having sizes 1.5d and d, The total length of cantilever is 150 mm, out of which first 50 mm is bigger (1.5d) and remaining 100 mm is smaller (d). The cantilver is attached at the bigger end. A force acts at free end in vertically downward direction, which varies from -50 N to +150 N.Determine the diameter of the beam d using modified goodman diagram. using
Factor of safety =2,
Reliability 90% { reliability factor 0.897}
Surface finish factor 0.77
Size factor 0.85
The notch sensitivity =0.9
Theorotical stress concentration factor =1.44
10) A cantilever of 30C8 material is subjected to a transverse load variying from 50 N to 150 N acting in downward direction. It is also subjected to an axial load varying from 150 N compression to 500 N tensile. The total length of cantilever is 175 mm out of which first 50 mm has diameter 2d and remaining 125 mm has diameter d. The bigger part is attached to wall and smaller end is free end. Find the dimension d for an infinite life if Su=560 MPa, Se=280 MPa,Ka=0.8,Kb=0.85, Kc=0.7 for axial load and Ka=0.8,Kb=0.8,Kc=1 for bending. Reliability factor is 0.987 . Take the fos 2.5 for both type of loading.
- Log in to post comments
