Theory Questions and Answers on Sliding Contact Bearings

Q.1. State the Assumptions made in Petroff's equation. Derive the Petroff's equation. Also state the limitations of PEtroff's equation.

Ans :

Petroff equation is used to determine the coefficient of friction in hydrodynamic bearing, it is based on following assumptions,

1. The journal (shaft) is concentric with the bearing.

2. The bearing is subjected to light low.

3. The journal (shaft) speed is very high.

4. The viscosity of the fluid is high.

Derivation :

Consider a horizontal shaft rotating in the bearing as shown in figure

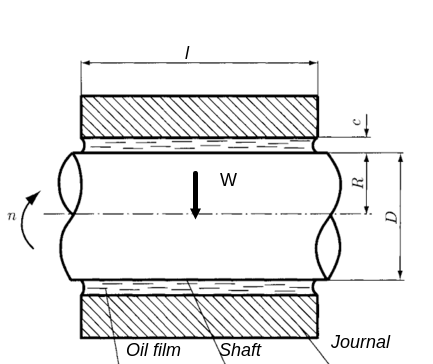
the shaft is concentric with the bearing, with usual notations let,

r= radius of journal ( shaft) in millimetres

R = radius of the bearing in millimetres

l= length of the bearing in millimetres

c = radial clearance between the journal and the bearing c=R-r,

ns= speed of the shaft in revolutions per second

V= velocity at surface of journal in millimetres per second,

u= absolute or dynamic viscosity of fluid in N-s/mm2

W= in radial load on the journal in N

pb= bearing pressure on projected area in Newton per mm square,

The tangential frictional force acting on journal due to viscous drag is given by Newton's law of viscosity,

$F= \mu \times A \times \frac{dv}{dh } = \mu \times (2 \pi r l) \times \frac {V}{v}$

$F = \mu \times (2 \pi r l) \times \frac {2 \pi r n_s }{c}$

The Frictional torque acting on the journal due to viscous drag is given by,

$T =F . r= \mu \times (2 \pi r l) \times \frac {2 \pi r n_s }{c} \times r$

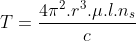$T = \frac{4 \pi^2 .r^3 .\mu . l. n_s}{c}$ ....................................(1)

The equation gives the frictional torque due to viscous drag and it can be expressed in terms of equal and coefficient of friction of the bearing,

The frictional torque can also be expressed as ,

$T =f .W. r$ f= Coefficient of friction ,

$T =f .(P_b . 2r . l). r$

$T =2 f .P_b . r^2 . l$ .................................(2)

Combining the equation 1 and 2 for torque,

$2f. p_b.l.r^2 = \frac{4 \pi^2. r^3. \mu. l. n_s}{c}$

Rearranging the terms,

$\mathbf{{\color{Red}f = 2 \pi^2 . \left ( \frac{r}{c} \right ). \left ( \frac{\mu . n_s}{p_b} \right ) }}$

This equation is known as Petroff's equation..

Limitations of petroff's equation :

the assumptions made in deriving the petroff's equation do not exist in actual practice, whereas now a days advanced data of the hydrodynamic bearing is available, so the petroff's equation is rarely used.

Q.2. State the Assumptions made in deriving Reynold's equation, Also write Reynold's equation for 2D Flow.

Ans :Reynolds equation is based on the following up assumptions,

1.The fluid or lubricant base Newton's law of viscosity.

2. The fluid or weekend is incompressible.

3. The inertia forces in the flight film are negligible.

4. The flow of fluid or lubricant is laminar.

5. The viscosity of fluid of lubricant is constant throughout the film.

6. The pressure of the lubricant is constant along the film thickness.

7. The shaft and bearing are rigid.

8. The effect of curvature of the film is neglected since the fluid film thickness is very small as compared to the bearing radius.

Reynolds equation for two dimensional flow

${\color{Red} \mathbf{\frac{\partial }{\partial x} \left [ h^3 .\frac{\partial p}{\partial x} \right ] +\frac{\partial }{\partial z} \left [ h^3 .\frac{\partial p}{\partial z} \right ] =6\mu U\left [ \frac{\partial h}{\partial x} \right ]}}$

Q.3. What is Hydrodynamic and Hydrostatic lubrication ?

Ans ; Hydrodynamic Lubrication :

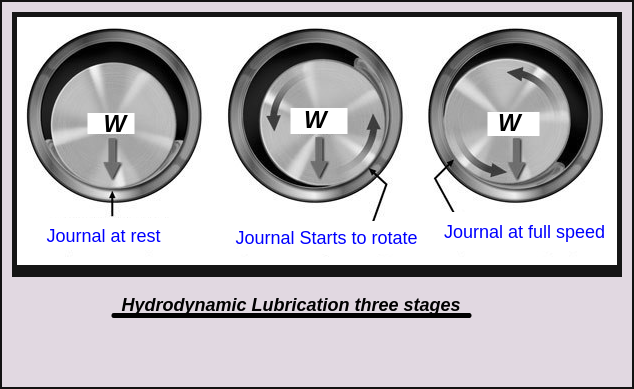
"Hydrodynamic lubrication is defined as a system of lubrication in which the fluid film is created by the shape and relative motion of the sliding surfaces." in other words no external sources required to create oil wedge between journal and bearing. in this type of lubrication pressure is generated within the system. figure below shows the three positions of the journal and bearing.

Hydrostatic Lubrication:

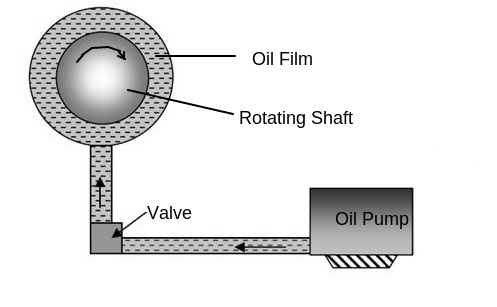
"Hydrostatic lubrication is defined as a system of lubrication in which the flight free is created by use of an external source which supplies the lubricant under pressure."this type of lubrication is also called externally pressurized bearing. Hydrostatic bearings offer the following advantages

Hydrostatic bearings offer the following advantages

1. Hydrostatic bearings have high load carrying capacity even at low speeds.

2. There is no starting friction in hydrostatic bearings.

3. There is no friction and rubbing action at any operating speed or load.

Q.4.write a short note on selection of hydrodynamic bearing design variables or explain in brief design variables and performance variables of hydrodynamic bearing.

Ans : following are the various variables related to hydrodynamic bearing, variable grouped into two categories called design variable and performance.

Design variables : the variables which are under the control of designer design variables. following are the four important design variables,

1) Speed of journal

2) Viscosity of fluid

3) Load per unit projected area

4) Bearing dimensions such as radius, length and clearance.

out of the above variables the speed of the journal is actually specified by the application itself so it is not in total control of the designer of bearing.

Performance Variables : the variables which are used to analyse the performance of the bearing are called performance variables, these variables include

1) coefficient of friction

2) minimum oil film thickness

3) temperature rise of the fluid

4) flow rate of lubricant

The designer can indirectly control these performance variables by changing one or more of the design variables. these variables are very important for satisfactory performance of the bearing.

Q.5.Explain raimondi and boyd method for design of hydrodynamic journal bearing.

Ans : The theory of hydrodynamic lubrication is based on a differential equation which is derived by Reynolds, the equation is given as,

There is no exact analytical solution to this differential equation, however A A Raimondi and John Boyd solve this equation using iterations technique. as a result of their solution the expressed the performance of hydrodynamic bearing in terms of certain dimensionless parameters. these dimensionless parameters are made by combining different design and performance variables, this dimension list parameters are available in the form of charts of tables. the charts and tables are available for full and partial journal bearings having l/d ratios as $\infty ,1,1/2,1/4$ .

the table provides the following dimensionless parameters,

eccentricity ratio = $\varepsilon$

minimum film thickness variable = $\frac{h_o}{c}$

sommerfeld number =S

angle of eccentricity = $\phi$

coefficient of friction variable = $(\frac{r}{c})f$

flow variable= $(\frac{Q}{r..cn_s.l})$

side leakage ratio = $(\frac{Q_s}{Q})$

pressure ratio = $(\frac{P}{P_{max}})$

Following are the Numerical collected from Various Universities

1) Following data is given for a full hydrodynamic bearing:
Journal diameter=100mm
Bearing length=50mm
Journal speed=1500rpm
Viscosity of lubricant=30cP
Minimum film thickness=15 microns
Specific gravity of lubricants=0.86
Specific heat of lubricants=2.09kJ/kg°C
The fit between the journal and bearing=H 7 e 7

Calculate:
i) Load carrying capacity of the bearing,

ii) Side Leakage; and
iii) temperature rise, considering the effect of side leakage.
Using the following data:

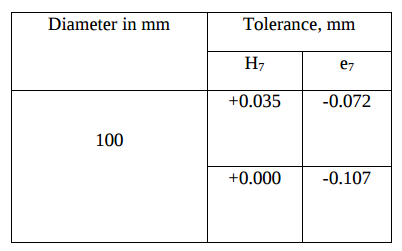
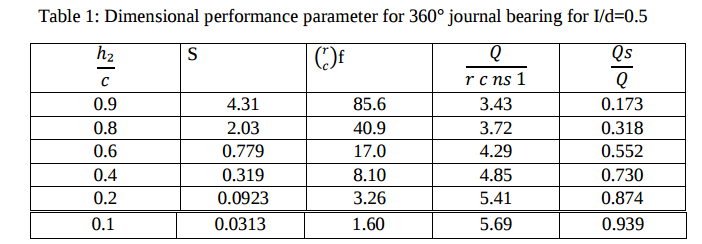
2) The following data is given for 360° hydrodynamic bearing :
• Radial load = 3 kN
• Journal diameter = 50 mm
• Bearing length = 50 mm
• Journal speed = 1490 rpm
• Radial clearance = 50 microns
• Viscosity of lubricant = 23.4375 cP.

Calculate Minimum oil film thickness, coefficient of friction, power lost in friction and flow rate.

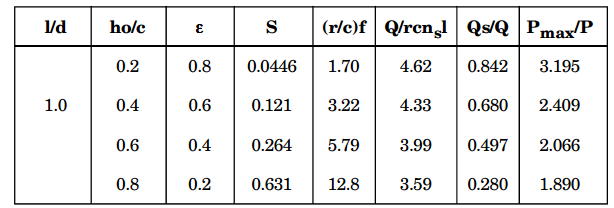
3) The following data is given for a full, hydrodynamic bearing:

Journal speed: 1440 rpm,

Journal diameter: 60 mm,

Bearing length: 60mm,

radial clearance: 0.06mm,

radial load: 3 kN,

viscosity of lubricant: 30 cP.

Assume that total heat generated due to friction in bearing is carried by
the total lubricant flow. Calculate:
i) Coefficient of friction
ii) Minimum oil flim thickness
iii) Flow requirement
iv) Temperature rise
v) Power lost in friction.

4) Following data is given for a full hydrodynamic bearing:
Radial load: 22 kN, journal speed: 960 rpm, Unit pressure in bearing: 2.4 MPa, l/d = 1:1, viscosity of lubricant = 20 cP, Ratio of h o /c = 0.2 = (Minimum oil thickness)/(radial clearance)

Determine:
i) Dimensions of bearing
ii) Minimum film thickness
iii) Requirements of oil flow

5) The following data is given for a 360° hydrodynamic journal bearing,
radial load - 6.5 kN, journal speed - 1200 rpm, journal diameter - 60 mm,
bearing length - 69 mm. minimum oil film thickness 0.009 mm. The fit between journal and bearing is normal fit H 7 e 7 for which hole diamter is 60 + 0.00/+0.03 and shape diameter 60 −0.06/-0.09 specilty the viscosity of lubricating oil for given journal bearing.

6) A hydrodynamic journal bearing is to be designed to support a radial load of 5 kN. The l/d ratio to be considered is 0.4. The journal rotates at 5040 rpm. The eccentricity ratio is 0.6. If central lubrication supplies lubricating oil of viscosity 46 C. Poise (cP) at flow rate of 0.5 1it/min to bearing. Calculate

i) Diameter of journal
ii) Radial clearence
iii) Dimensions of Bearing
iv) Minimum oil film thickness.

7) Following data is given for a 360 o hydrodynamic bearing.
Radial load = 10kN,
Journal speed = 1440 rpm,
Unit pressure in bearing = 1000 KPa,
Clearance ratio (r/c) = 800
l/d = 1
Viscosity of lubricant = 30 mPa-S.
Assuming that total heat generated in the bearing is carried by the total oil flow
in the bearing. Calculate
a) Dimensions of bearings
b) Coefficient of friction
c) Power lost in friction
d) Total flow of oil
e) Side leakage
f) Temperature rise
g) Average temperature (inlet temperature is 40 o C)
h) Find maximum pressure (P max )

8) The following data is given for a 360° hydrodynamic bearing:
Radial load = 9 KN
Unit bearing pressure = 900kPa
Clearance ratio = (r/c) = 800
Journal speed = 1440 rpm
Viscosity of lubricant = 30 mpas
Assume that the total heat produced in the bearing is carried by the total oil flow and 1/d is equal to 1. Calculate dimensions of the bearing, coefficient of friction, power lost in friction, total flow of oil, side leakage
and temperature rise. Refer Table for bearing data.

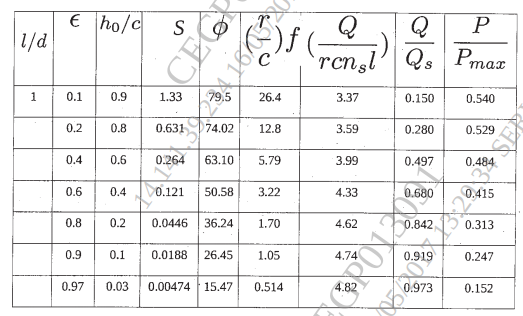
9) Design a full hydrodynamic journal bearing with the following specification
for machine tool application:
Journal diameter = 75 mm

Radial load = 10 KN

Speed of journal : 1440 rpm

Minimum thickness of oil film : 25.5 micron

Permissible unit bearign pressure : 2 N/mm2

Radial clearance = 0.001mm

Inlet temp = 40 degrees

Mass density of lubricant = 860 kg/m3

Bearing material is Babbit

Specific heat = 1.76 KJ/Kg K

Find the length of bearing and select Suitable oil for the given application

Use the following table...

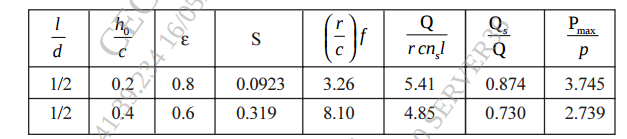
10) The following data is given for 360° hydrodynamic bearing:
Journal diameter 100 mm
Bearing length 50 mm
Journal Speed 1440 rpm
Minimum oil-film thickness 15 microns
Viscosity of lubricants = 30 CP
Specific gravity of lubricant = 0.86
Specific heat of lubricant = 2.09 KJ/kg°C
Fit between the journal and bearing is normal running fit H 7 e 7 .

Calculate ,
1) The coefficient of friction;
2) The power lost in friction;
3) The load carrying capacity of bearing;
4) The total flow requrement of lubricant

You are here

Sliding Contact Bearings : Theory Q&A