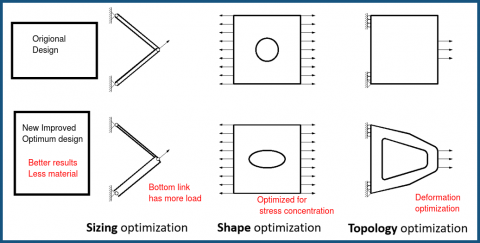
Optimum Design : Theory Questions, Answers, Numerical Problems
Optimum design related key Notes to remember
- Optimum is the golden mean of maximum and minimum.It is a challenge for Designer to design an efficient as well as cost effective system without compromising their integrity, this task is faciliated by optimum design.
- An optimum design means the best or the most suitable of all the feasible conceptual designs.
- Adequate design is the design which fulfils the main functional requirement of the component.
- Optimum designis inclusive of adequate design
- For a component there can be several aqequate designs, but there is only one optimum design.
Questions and Answers on Optimum design.
Q.1. Define adequate design & optimum design.
Ans : Adequate design:
Adequate design is the selection of material & the values for independant geometrical parameters for a mechanical elements such that the mechanical element satisfies its function requirement & the undesirable effects are kept in tolerable limit. For example if one wants to design a shaft for a machine. The maerial for tha shaft will be selected from the list of feasible materials and the geometrical parameter (Dia of shaft) will be determined on the basis of strength equation based on stress or rigidity. One will get different sizes for the different materials choosen. All such designs are known as adequate design.
Optimum Design:
Optimum design is th selection of material & the values for independant geometrical parameters with the explicit objective of either minimizing most significant undesirable effects or maximizing most significant functional requirement while making certain that the mechanical element satisfies function requirement & other undesirable effects are kept within tolerable limits. For example if one wants to design a shaft for a machine with "Minimum weight criteria for that particular application" then there will be a single solution out of various options available. Such design is called optimum design.
Optimum design is inclusive of adequate design.
Q.2. Explain the various design parameters. Or Explain Functional requirement parameters,Material parameters and Geometric parameters.
Ans :The design parameter that make the design complete and successful are classfied into three groups
1) Functional requirement parameters : These are the conditions imposed by the end applications on the component. These are the requirements which are must for the proper functioning of the component. Generally functional requirement parameters are independent of the material or geometric parameters
2) Material Parameters : The material parameters are those parameters which describe the material with values. like density, modulus of elasticity, modulus of rigidity, yield strength, ultimate tensile strength, cost per kg etc
3) Geometrical parameter : These are the parameters which define/limit the geometry of the mechanical component. like module of gear, length of belt, face width of gears etc.
Q.3. Explain desirable and undesirable effects in optimum design. or Explain the functional requirement parameter in optimum design.
Ans : The functional requirements are the conditions which must be satisfied by the mechanical element so that it works as intended. The functional requirements are classified classified as Desirable and Undesirable effects
Desirable effects : Desirable effects are the functional requirement parameters that are useful for the mechanical element to perform satisfactorily its function, like tensile strength, power transmitting capacity, storage capacity , bending resistance etc. Desirable effects are best when they are maximum in value
Undesirable effects : Undesirable effects are also functional requirements but which are detrimental for its functioning, and are best when they have minimum in value. Like weight of component, cost of component, Imbalance in component etc.
Q.4. What are the objectives of optimum design?
Ans : For a design problem a large number of solutions are available which basically fulfil the functional requirement. Optimum design helps to choose the best alternative of the all available keeping a certain target in mind like minimizing weight or maximum strength or minimum cost . Following are the main objectives
1) To select the best possible option from the available alternatives keeping the target of maximizing a desirable effect or minimizing the undesirable effect
2) To reach the best solution without doing the repetitive work of detail analysis and evaluation of each alternative ( If the optimum design methods would not be there, we would have to desing complete component considering each alternative material and then after lot of labourious work we would reach a conclusion)
Q.5. Explain Johnsons Method of Optimum Design.
Ans :Johnson's method involves developing three major design equations and solving these equations. These three equations are
1) Primary design equation(PDE) : It is most important equation which outlines the most significatn functional requirement to be maximized or the most significant undesirable effect which is to be minimized. For example in design of a tensile bar the primary target of minimum weight, then the equation for weight is the PDE.
2) Secondary design equation ( SDE ) The secondary or subsidiary design equation are the important equation other than the primary design equation. For example in case of tensile bar design the equation of tensile stress is the SDE.
3) Limit Equation (LE) : The limit equatins are the important design equation that define the satisfactory ranges of certain design parameters. Like the limiting value of stress, or torsional stiffness etc.
Following steps are followed in optimum design using Johnsons Method for normal specifications
- Select independent geometrical parameters
- Decide the basis of optimum design (like weight,cost,strength etc)
- Write P.D.E
- Write S.D.E and L.E
- Classify parameters
- Combine S.D.E 's with P.D.E's
- Find variation of optimum design quantity
- Impose L.E. on P.D.E
- Write final P.D.E in terms of parameter groups
- Select optimum material from comparison table for various materials
- Determine optimum values of geometrical parameters
1) A cantilever beam is having length of 250 mm and is rectangular in cross section is subjected to a varying load of magninude. Th ratio of width to depth for the beam is 5:1. If the factor of safety is 3, Design the beam for the optimum material cost and find the suitable dimensions of the beam.
Use the following materials
| Material | Mass Density in kg/m3 | Matrial cost per unit weight in Rs/N | Endurance Limit ‘Se’ in N/mm2 |
|---|---|---|---|
| M1 | 8450 | 100 | 17 |
| M2 | 8020 | 100 | 37.5 |
| M3 | 7830 | 60 | 32 |
2) A tebsile bar of crosssectional area of 85 mm2v (at least) and has length of 200 mm is subjected to a constant load of 500 N. Design the bar with minimum cost of the following material, taking the factor of safety 2. Use the following materials
| Material | Mass Density in kg/m3 | Matrial cost per unit weight in Rs/N | Yield strength MPa |
|---|---|---|---|
| M1 | 7500 | 16 | 130 |
| M2 | 3100 | 32 | 50 |
| M3 | 2100 | 32 | 20 |
3)A shaft is required in a lightweight equipment to transmit 40 KW at 425 rpm. The required stiffness of shaft is to be taken as 90 N-m/degree. the F.O.S based on yield strength in shear is 1.5. Using the maximum shear stress theory, design the shaft with the main objective of “MININUM WEIGHT” using the following materials
| Material |
Mass density Kg/M3 |
Material cost per unit weight C Rs/N |
Tensile Yield strength Syt in N/mm2 |
Modulus of Rigidity G, N/mm2 |
|---|---|---|---|---|
| Alloy steel | 7800 | 7.5 | 450 | |
| Aluminium alloy | 2800 | 9 | 150 | |
| Titanium alloy | 4500 | 150 | 800 | |
| Magnesium alloy | 1800 | 10 | 100 |
4)Design a tensile bar 200mm long required to carry 5 kN of tensile load that would ‘COST’ the least among the following available options
| Material |
Mass density Kg/M3 |
Material cost per unit weight C Rs/N |
Tensile Yield strength Syt in N/mm2 |
|---|---|---|---|
| Steel | 7500 | 16 | 130 |
| Al alloy | 3000 | 32 | 50 |
| Ti alloy | 4800 | 480 | 90 |
| Mg alloy | 2100 | 32 | 20 |
5)A tensile bar having length 500 mm carries a tensile force of 3 kN. Taking the factor of safety as 2, design the bar with objective of ‘MININUM COST’, out of the following materials,
| Material |
Mass density Kg/M3 |
Material cost per unit weight C Rs/N |
Tensile Yield strength Syt in N/mm2 |
|---|---|---|---|
| Al Steel | 7800 | 28 | 400 |
| Al alloy | 7850 | 150 | 900 |
| Ti alloy | 2800 | 132 | 150 |
| Plain Carbon Steel | 4500 | 2200 | 800 |
6) A Shaft is required to transmit a power of 100 KW and running at 100 revolutions per minute. The torsional stiffness for the shaft is 90 N-m /degree. Design the shaft using Maximum shear stress theory and with prime consideration of “MINIMUM WEIGHT”. Material properties are given below. Also determine the diameter and length of shaft for the same. Assume the FOS 1.5 and Combined shock and fatigue load factor as 1.5
| Material | Mass Density in kg/m3 | Matrial cost per unit weight in Rs/N | Modulus of Rigidity MN/mm2 |
|---|---|---|---|
| M1 | 7800 | 450 | 82000 |
| M2 | 2800 | 150 | 27000 |
| M3 | 1800 | 100 | 17000 |
7) A tensile rod having diameter d and length 0.6 meters is subjected to a force of 5000 Newtons. Find the rod diameter with the prime objective of “Minimizing Weight”, choose from the following materials. Use factor of safety as 2.
| Material |
Mass density Kg/M3 |
Material cost per unit weight C Rs/N |
Tensile Yield strength Syt in N/mm2 |
Modulus of Rigidity G, N/mm2 |
|---|---|---|---|---|
| Steel | 7800 | 7.5 | 400 | |
| Aluminium alloy | 2800 | 9 | 150 | |
| Titanium alloy | 4500 | 150 | 800 |
8) A tension bar having crosssectional diameter of 85 mm and 200 mm long is subjected to load of 5 KN.Design the shaft with prime consideration of “Minimum Cost”. Assume a suitable factor of safety.
| Material |
Mass density Kg/M3 |
Material cost per unit weight C Rs/N |
Tensile Yield strength Syt in N/mm2 |
|---|---|---|---|
| Al Steel | 7500 | 16 | 130 |
| Al alloy | 3000 | 32 | 50 |
| Mg alloy | 2100 | 32 | 20 |
9) A cantilever beam is having length 250mm and rectangular cross section is to act as a spring subjected to a load which varies in the range of . The width of beam is 5 times its depth. If FOS is to be taken as 1.5, design the beam for “OPTIMUM MATERIAL COST”. Specify material, cross-section and cost for selected design. The following material are available for evaluation
| Material | Mass Density in kg/m3 | Matrial cost per unit weight in Rs/N | Endurance Limit ‘Se’ in N/mm2 |
|---|---|---|---|
| M11 | 8450 | 100 | 17 |
| M12 | 8020 | 100 | 37.5 |
| M13 | 7830 | 60 | 32 |
10) A shaft transmits a troque of 1500 N-m and is required to have torsional stiffness of 100 N-m/degree. Using the maximum shear stress theory as basis and FOS 2 based on yield strength in shear, design the shaft with objective of “Mininum weight” out of the following materials.
| Material |
Weight density N/M3 |
Tensile Yield strength Syt in N/mm2 |
Modulus of Rigidity G, N/mm2 |
|---|---|---|---|
| M1 | 77000 | 420 | |
| M2 | 76500 | 230 | |
| M3 | 44000 | 900 | |
| M4 | 17500 | 225 |
11) A tensile bar having length 300mm is subjected to constant tensile force of 7.5 kN. If the factor of safety is 4, design the bar, use Johnsons method of optimum design, with the objective of “Minimum material Weight” using optimum material from the list given below.
| Material |
Mass density Kg/M3 |
Material cost per unit weight C Rs/N |
Tensile Yield strength Syt in N/mm2 |
|---|---|---|---|
| Steel | 7500 | 28 | 400 |
| Aluminium alloy | 2800 | 132 | 150 |
| Titanium alloy | 4500 | 2200 | 800 |
12) Design a shaft with “Minimum Weight” as the prime criterion. The shaft is required to transmit a torque of 900 N-m and it should have torsional stiffness as 60 N-m per degree. Use factor of safety of 1.5 based on Yield strength. Use Maximum Shear stress theory of failure for design. Use the following materials
| Material |
Mass density Kg/M3 |
Material cost per unit weight C Rs/N |
Tensile Yield strength Syt in N/mm2 |
Modulus of Rigidity G, GPa |
|---|---|---|---|---|
| Material 1 | 8500 | 16 | 130 | 80 |
| Material 2 | 3000 | 32 | 50 | 26.5 |
| Material 3 | 4800 | 480 | 90 | 40 |
| Material 4 | 2100 | 32 | 20 | 16 |
What will be the desing if the criterion for design is changed to “Minimum cost” ?
13) A thin spherical vessel is to be designed with objective of max storage capacity, which is given by , where D is the diameter of the vessel. The vessel is subjected to internal pressure of 5 N/mm2 and the FOS based on yield strength is 2. Design the vessel using following materials. Mass of empty vessel should not exceed 150 kg.
| Material |
Mass density Kg/M3 |
Tensile Yield strength Syt in N/mm2 |
|---|---|---|
| Steel | 7500 | 450 |
| Aluminium alloy | 2800 | 150 |
| Titanium alloy | 4500 | 800 |
| Magnesium alloy | 1800 | 100 |
14) A cantilever beam having rectangular cross-section is 200 mm long. Widsh of beam is five times its depth. It is required to function as a spring member in a device. It is subjected to vertical force which acts at free end and whose magnitude varies . The maximum deflection at the free end is limited to 1 mm. Using FOS as 2 determine the dimensions of beam with prime criterion of “ Minimum material cost” Out of the following available materials.
| Material |
Mass density Kg/M3 |
Material cost per unit weight C Rs/kg Weight |
Modulus of elasticity in N/mm2 |
Endurance limit in N/mm2 |
|---|---|---|---|---|
| Material 1 | 7800 | 20 | 207000 | 130 |
| Material 2 | 2800 | 70 | 72000 | 50 |
| Material 3 | 4500 | 800 | 114000 | 260 |
Links to other topics in Mechanical System Design
- Log in to post comments
