Graphical Solution for Angular Velocity in a Four-Bar Chain

By user , 17 November 2025

Problem Statement

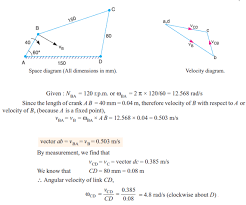
In a Four-bar chain ABCD, $AD$ is fixed and is $150 mm$ long. The crank $AB$ is $40 mm$ long and rotates at $120 r.p.m.$ clockwise, while the link $CD = 80 mm$ oscillates about $D$ . $BC$ and $AD$ are of equal length. Find the angular velocity of link $CD$ when angle $∠BAD = 60°$ .

1. Given Data and Initial Calculations

Link	Length (m)	Other Data
Fixed Link (AD)	$L AD = 0.15 m$	$N AB = 120 r.p.m.$ (CW)
Crank (AB)	$L AB = 0.04 m$	$∠BAD = 60°$
Coupler (BC)	$L BC = 0.15 m$
Rocker (CD)	$L CD = 0.08 m$

four-bar-chain-abcd-ad-fixed-and-150-mm-long-crank-ab-40-mm-long-and-rotates-120-rpm-clockwise-while

Analytical Calculations (Crank AB)

**1. Angular Velocity of Crank AB (ω_AB):** $ω AB = (2 π N AB) / 60$
$ω AB = (2 π \times 120) / 60 = 4 π rad/s \approx 12.57 rad/s$

**2. Linear Velocity of Point B (V_B):** $V B = ω AB \times L AB$
$V B = 12.57 rad/s \times 0.04 m = 0.5028 m/s$

2. Calculation of Angular Velocity (ω_CD)

Assuming the linear velocity of $C$ ( $V C$ ) is found graphically, the final angular velocity of link $CD$ ( $ω CD$ ) is calculated using the relationship:

Graphical Solution for Angular Velocity in a Four-Bar Chain

Problem Statement

1. Given Data and Initial Calculations

Analytical Calculations (Crank AB)

2. Calculation of Angular Velocity (ωCD)

Comments

2. Calculation of Angular Velocity (ω_CD)