(a) Define : (i) Spherical pair (ii) Higher pair
a) Single plate clutch b) Multi plate clutch c) Cone clutch d) Centrifugal clutch
ii) Classification of follower:
Theory
A single plate clutch, effective on both sides, is required to transmit 25 kW at 3000 rpm. Determine the outer and inner radii of frictional surface, if the co-efficient of friction is 0.255 the ratio of radii is 1.25 and the maximum pressure is not to ex
A simple band brake is operated by lever 40 cm long. The brake drum diameter is 40 cm and brake band embrance 5/8 of its circumference. One end of band is attached to a fulcrum of lever while other end attached to pin 8 cm from fulcrum. The co-efficient o
Simple band brake:
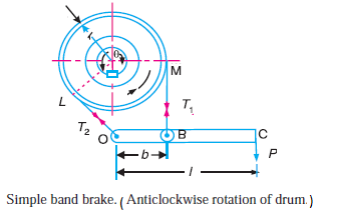
Given: Length of lever l = 40 cm = 0.4m, diameter d = 40 cm = 0.4, µ = 0.25, b =0 .08 m ϴ = Angle of wrap = 5/8 x 360 = 225 x π /180 = 3.93 rad Braking torque = (T1 –T2) x r T1/T2 = e µϴ = e 0.25 x 3.93 = 2.67 Taking moments about fulcrum P x l = b x T1 500 x 0.40 = 0.08 x T1 T1 = 2500 N T2 = 2500 / 2.67 = 936.3 N Braking Torque = (2500 – 936.3) x 0.2 = 312.74 N-m
Draw turning moment diagram for single cylinder four stroke I.C. Engine.
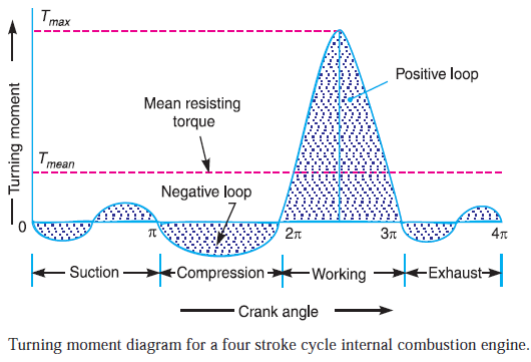
ii) Turning Moment Diagram:
State types of gear train and explain any one.
i) Types of gear trains 1) Simple gear train 2) Compound gear train 2) Epicyclic gear train 4) Inverted gear train Simple gear train. When there is only one gear on each shaft, it is known as simple gear train. The gears are represented by their pitch circles. When the distance between the two shafts is small, the two gears are made to mesh with each other to transmit motion from one shaft to the other Epicyclic gear train: A simple epicyclic gear train is shown in Fig. where a gear A and the arm C have a common axis at O1about which they can rotate.
Two pulley, one 450 mm diameter and the other 200 mm diameter are on parallel shafts 1.95 m apart and are connected by a crossed belt. Find the length of the belt required and the angle of contact between the belt and each pulley. What power can be transm
Draw the profile of a cam to raise a valve with S.H.M. through 40 mm in of revolution, keep it fully raised through 1/10 th 1 th 4 revolution and to lower it with uniform acceleration and retardation in 1/6 th revolution. The valve remains closed during t
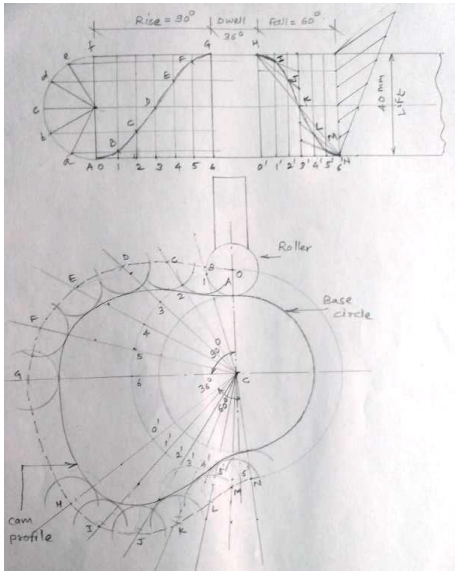
Fig shows a displacement diagram and a cam profile for the roller follower.
The crank of a slider crank mechanism rotates clockwise at a constant speed of 300 rpm. The crank is 150 mm and the connecting rod is 600 mm long. Determine : (i) linear velocity and acceleration of the mid-point of the connecting rod, and (ii) angular ve
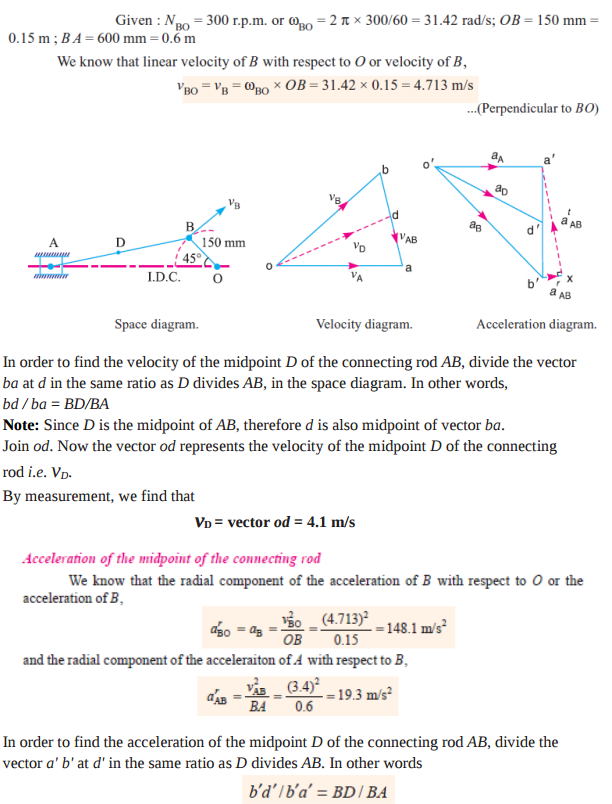
Note: Since D is the midpoint of AB, therefore d' is also midpoint of vector b' a'. Join o' d'. The vector o' d' represents the acceleration of midpoint D of the connecting rod i.e. aD.
By measurement, we find that aD = vector o' d' = 117 m/s2
Given: Lift = 40 mm Rise = ¼ x 360 = 900 Fall =1/6 x 360 = 600 Dwell = 1/10 x 360 =360
Four masses attached to a shaft and their respective radii of rotation are given as : m 1 = 180 kg m 2 = 300 kg m 3 = 230 kg m 4 = 260 kg r 1 = 0.2 m r 2 = 0.15 m r 3 = 0.25 m r 4 = 0.3 m The angles between successive masses are 45, 75 and 135. Find th
Given : m1 = 180 kg, m2 = 300 kg, m3 = 230 kg, m4 = 260 kg r1 = 0.2 m, r2 = 0.15 m, r3 = 0.25 m, r4 = 0.3 m ϴ1 = 45, ϴ2 = 75, ϴ = 135 The centrifugal forces are given by - m1r1 = 36, m2r2 = 45, m3r3 = 57.5, m4r4 = 78
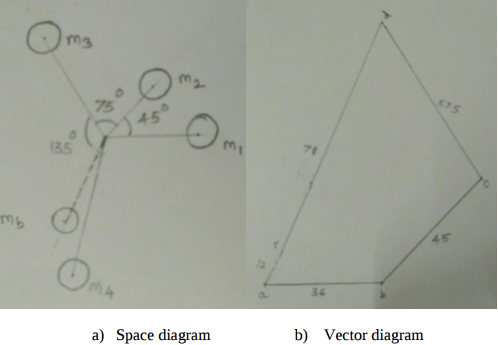
From vector diagram the resultant force is at 60 to the mass m1 and is represented by ar ar = 12 kg m Therefore mb * rb = 12 kgm Balancing mass mb = 12/0.2 = 60 kg at an angle of 2400 with the direction of m1 mass
A flat foot step bearing 225 mm in diameter supports a load of 7500 N. If the co-efficient of friction is 0.09 and the shaft rotates at 600 rpm, calculate the power lost in friction.
Problem on Foot step bearing D = 225 mm = 0.225 m W = 7500 N µ = 0.09 N = 600 rpm ω = 2 π N / 60 =62.83 rad/sec Uniform pressure condition Frictional torque T = 2/3 µ W R = 50.625 Nm Power lost in friction = T x ω = 50.625 x 62.83 = 3180.8 W --------Ans Uniform wear condition Frictional torque T = 1/2 µ W R = 37.98 Nm Power lost in friction = T x ω = 37.98 x 62.83 = 2385.57 W -------- Ans
Pages
